МАТЕМАТИЧЕСКОЕ ПРИЛОЖЕНИЕ
I. О СВЯЗИ КАТЕГОРИЙ БЕСКОНЕЧНОСТИ,
ДВИЖЕНИЯ И СОВПАДЕНИЯ ПРОТИВОПО-
ЛОЖНОСТЕЙ
Поскольку понятие бесконечности исключительно важно для новоевропейской культуры в целом, то необходимо, следуя примеру Николая Кузанского и Блеза Паскаля, напомнить о некоторых математических аспектах этого понятия. Это представляется целесообразным, так как математика — наиболее строго, последовательно и отчетливо построенная наука; если ясность вообще возможна, то, конечно, прежде всего она возможна в математике.
Рассмотрим два конечных множества: множество трех крестиков и множество пяти ноликов. Сравним количества элементов в этих множествах:
ХХХ меньше элементов
ООООО больше элементов
Можно утверждать, что ноликов больше. Почему? Потому что, устанавливая взаимно однозначное соответствие между крестиками и ноликами, мы используем все крестики, а два нолика останутся. Значит, ноликов на два больше. Итак, понятия больше и меньше применительно к конечным множествам имеют отчетливый смысл.
Рассмотрим теперь натуральный ряд — ряд целых положительных чисел: 1, 2, 3, 4, …. Построим еще один ряд, который получается из натурального ряда умножением на два. Предположим, что мы оборвем оба ряда на числе 6:
1 2 3 4 5 6 множество (целое)
2 4 6 его подмножество (часть)
Нижнее множество (2, 4, 6) меньше верхнего (1, 2, 3, 4, 5, 6). Все числа, входящие в меньшее множество, входят и в большее, но не все, входящие в большее, входят в меньшее. Множество (2, 4, 6) есть часть (подмножество) множества (1, 2, 3, 4, 5, 6), которое в данном случае выступает как целое.
В философии часть и целое рассматривают как противоположности. Одна из аксиом геометрии Евклида гласит: целое больше своей части (Киселев А. П. Геометрия. Учебник для IX–X кл. М., 1971. Ч. 2. Стереометрия. С. 93) (и это безусловно верно для конечных объектов).
Натуральный ряд, как известно, бесконечен (пример бесконечного множества):
…….. — бесконечное множество (целое) 2 4 6 8 10 12……. — его подмножество (часть)
Если мы не будем обрывать верхний ряд на каком- либо числе, а устремим его в бесконечность, то взаимно однозначное соответствие между элементами множества и подмножества нигде не нарушится, хотя вполне очевидно, что верхний ряд — целое, а нижний — часть целого. Итак, бесконечное множество (верхний ряд) эквивалентно своему подмножеству (нижний ряд); часть бесконечного может быть равна целому (т. е. противоположности совпадают) (Зигель Ф. Ю. Неисчерпаемость бесконечности. М., 1984. С. 13), а понятия “больше” и “меньше” утрачивают определенность.
“Любое бесконечное множество эквивалентно некоторому своему подмножеству, не совпадающему со всем множеством. Этот факт может быть принят за определение бесконечного множества” (Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть I. М., 1971. С. 87).
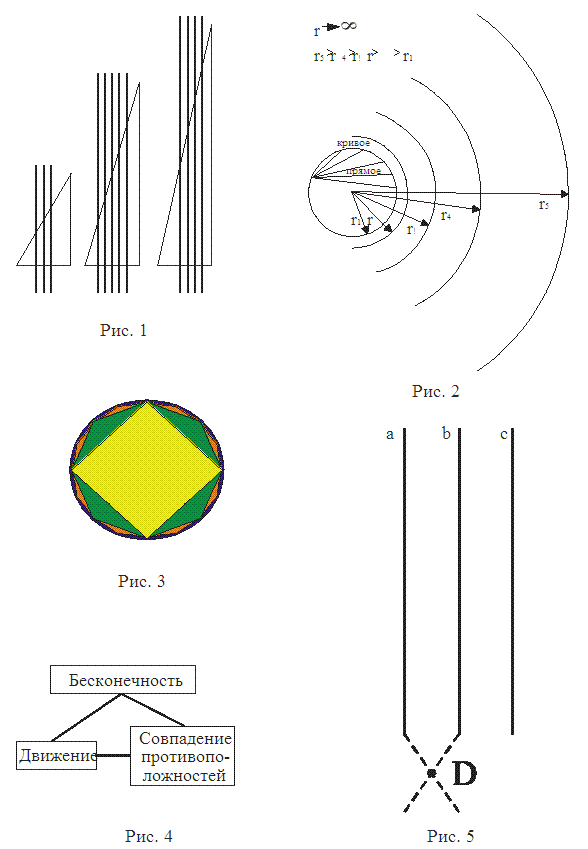
Со времен великого немецкого математика Георга Кантора (1845–1918) в математике различают бесконечные счетные множества (их элементы можно перенумеровать; примером такого множества является натуральный ряд) и бесконечные множества, обладающие мощностью континуума (примером такого множества может служить множество точек на отрезке прямой; это множество несчетно; перенумеровать его элементы (точки) невозможно) (Гарднер М. Математические новеллы. М., 1974. С. 123–136). Множества, обладающие мощностью континуума, тоже можно ставить в соответствие друг другу. Рассмотрим, например, прямоугольный треугольник, один из катетов которого имеет фиксированную длину, а другой катет и гипотенузу можно произвольно увеличивать (см. рис. 1). Пересе- чем катет постоянной длины совокупностью прямых, параллельных между собой и перпендикулярных к этому катету.
Каждая из прямых пересекает и катет, и гипотенузу, тем самым ставя одну из точек катета в соответствие одной из точек гипотенузы. Катет можно сделать сколь угодно малым, гипотенузу — сколь угодно большой, тем не менее взаимно однозначное соответствие точек катета точкам гипотенузы не нарушится. Итак, приходим к парадоксальному выводу: сколь угодно малая часть множества, обладающего мощностью континуума, может быть поставлена в соответствие всему множеству в целом (иначе говоря, сколь угодно малая часть множества, обладающего мощностью континуума, все-таки содержит бесконечно много точек!)
Рассмотрим математические построения выдающегося мыслителя эпохи Возрождения Николая Кузанского (1401–1464).
Прямое и кривое — пара противоположностей, отмеченная еще пифагорейцами [109, I, 31]. Рассмотрим окружность, в которой хорда (прямое) стягивает дугу (кривое) (см. рис. 2). Дуга совпадет с хордой в двух случаях:
• и дуга, и хорда станут бесконечно малыми, стянутся в точку (“Будь возможным начертить минимальную хорду, меньше которой не может быть, у нее не осталось бы излучины и она оказалась бы не меньше своей дуги: дойдя до минимального количества, хорда и дуга совпали бы” (Кузанский Н. Соч.: В 2 т. М., 1980. Т. 2. С. 440);
• радиус окружности станет бесконечно большим, и дуга станет неотличима от отрезка прямой.
В обоих случаях для совпадения противоположностей (лат. coincidentia oppositorum) необходима бесконечность в трактате “О геометрическом уме” встречаем понятие “двойной бесконечности”: “…обнаруживающиеся повсеместно бесконечности бесконечно большого и бесконечно малого. Действительно, каким бы быстрым ни было движение, всегда можно представить себе движение более быстрое, а это последнее в свою очередь ускорить, и так далее до бесконечности, нигде не встречая пределов ускорения1.
И, наоборот, каким бы медленным ни было движение, его можно замедлять, так и не достигая пределов замедления, бесконечно нисходя к той степени медленности, за которой начинается состояние покоя. Равным образом, как бы ни было число велико, можно вообразить еще большее, а затем и превосходящее его — и так бесконечно, не достигая числа, которое нельзя увеличить. И, напротив, каким бы оно ни было малым — сотая, десятитысячная доля — можно до бесконечности представлять себе еще меньшее, не достигая нуля или ничто (neant)… Одним словом, какими бы ни были движение, число, пространство и время, всегда можно говорить об их увеличении или уменьшении, так что расположенные между ничто и бесконечностью, они всегда удалены от этих пределов.
Такого рода истины нельзя доказать, однако они-то суть основание и начала геометрии. Поскольку же их недоказуемость обусловлена не затемненностью, а напротив, предельной очевидностью, отсутствие доказательств — не изъян, но, скорее, достоинство… Поистине, нелепостью будет утверждение, будто бы при непрестанном делении пространства наступает момент, когда, разделив очередной участок надвое, мы получаем неделимые и лишенные какой бы то ни было протяженности половины… Нет геометра, который не полагал бы пространство делимым до бесконечности” (Паскаль Б. Трактаты. Полемические сочинения. Письма. К., 1997. С. 78–82) (вспомните также фрагменты из книги Паскаля “Мысли”, помещенные в гл. 5).
Далее Паскаль указывает на то, что существование бесконечно больших и бесконечно малых величин взаимообусловлено.
Бесконечно большая величина — это величина, обратная бесконечно малой, и наоборот. Присутствие в математике нуля предполагает и обусловливает присутствие бесконечности. Античная математика (см. ниже) не знала ни нуля, ни бесконечности; новоевропейская математика немыслима без этих двух понятий.
Еще одна математическая аналогия Николая Кузанского относится к чрезвычайно важному для новоевропейской математики понятию предела (лат. limes) (Ильин В. А., Позняк Э. Г. Основы математического анализа: Ч. I. М., 1971). Последовательность периметров правильных n-угольников (где n = 3, 4, 5, ….) стремится к пределу, который равен длине окружности (см. рис. 3); однако предел этот достигается только в бесконечности (правильный многоугольник с бесконечным числом сторон).
В случае конечного n, каким бы большим оно ни было, периметр всегда меньше длины окружности. Такого рода последовательность, по мнению Николая Кузанского, иллюстрирует приближение к истине: ничто не познается так, чтобы нельзя было познать его еще совершеннее.
Математическое понятие предела родственно ключевым понятиям романтической эстетики — Sehnsucht и Streben (см. в гл. 6.: Реале Дж., Антисери Д. Западная философия от истоков до наших дней. Движение романтизма и его представители).
Таким образом, становится понятна мысль А. Лосева, характеризующего Романтизм как “беспокойно подвижную и неопределенно стремящуюся бесконечность” (Лосев А. Ф. Конспект лекций по эстетике нового времени. Классицизм // Лит. учеба. 1990. Кн. 4. С. 140) (см. также в гл. 6: Лосев А. Ф. Страсть к диалектике). Для постижения ключевой категории романтической эстетики — иронии — необходимы категории бесконечности, движения и единства противоположностей (Лосев А. Ф., Шестаков В. Н. История эстетических категорий. М., 1965).
Итак, было показано, что категории бесконечности и совпадения противоположностей движения (см. рис. 4). Что означает бесконечность натурального ряда? Она означает, что, как бы далеко мы ни продвинулись по натуральному ряду, каких бы больших чисел ни достигли, всегда можно продвинуться дальше. Как? Прибавив единицу к последнему построенному числу. Таким образом, бесконечность натурального ряда есть процесс построения все новых чисел, бесконечность натурального ряда означает возможность бесконечного движения по этому ряду2.
Гегель — завершитель немецкой классической философии. Идея единства (совпадения) противоположностей — самое сердце гегелевской диалектики. “Создание Гегелем логики становления явилось наивысшим достижением западной философии” [87, 134]. Гегель утверждает, что движение есть само существующее противоречие. Обратимся к исследованию простейшего случая движения — перемещение материальной точки в пространстве.
1. Рассмотрим покоящееся тело. На вопрос — находится ли это тело в точке А, или нет, можно дать однозначный ответ: да, находится, или — нет, не находится. Таким образом, рассуждение подчиняется центральному закону классической логики — закону исключенного третьего: из двух противоположных утверждений одно верно, другое ложно. В отношении одного и того же истинность А означает ложность не-А, и обратно, из ложности не-А следует истинность А (на этом основано доказательство от противного, лат. — reductio ad absurdum).
2. Рассмотрим движущееся тело. В этом случае ответ будет противоречивым: да, находится, и вместе с тем — нет, не находится. “Нечто движется не поскольку оно в этом “теперь” находится здесь, а в другом “теперь” там, а лишь поскольку оно в одном и том же “теперь” находится здесь и не здесь, поскольку оно в этом “здесь” одновременно и находится, и не находится. Надлежит согласиться с древними диалектиками, что противоречия, которые они нашли в движении, действительно существуют; но из этого не следует, что движения нет, а наоборот, что движение есть само существующее противоречие” (Антология мировой философии: В 4 т. М., 1971. Т. 3. С. 321–322).
Интересно соотнести это высказывание Гегеля с мыслью Платона, сформулированной им в диалоге “Кратил”: “…где всегда происходит изменяемость, там никогда не бывает знания…” (см. Введение). И Платон, и его учитель Сократ полагали, что знание об изменчивом (движущемся) невозможно, потому что попытка мыслить движение приводит к противоречию. Это очень ясно показано в знаменитых апориях Зенона Элейского, который, защищая учение Парменида, доказывает, что тезис о реальности движения приводит к логическим противоречиям3.
— “Ахиллес”, — формулируется таким образом: представим себе состязание в беге между быстроногим Ахиллесом и черепахой, бегущими в одном и том же направлении по двум параллельным дорожкам. Ахиллес дает черепахе фору, она стартует, например, с середины дистанции.
Зенон утверждает, что Ахиллес никогда не догонит черепаху. Он рассуждает так: за время, которое понадобится Ахиллесу, чтобы добежать до места старта черепахи, она тоже сдвинется на какое-то расстояние. К тому моменту, когда Ахиллес пробежит это расстояние, черепаха снова уйдет вперед. И так до бесконечности. Совершенно ясно, что рассуждение Зенона находится в вопиющем противоречии с реальностью (ведь на самом деле, конечно, Ахиллес догонит и перегонит черепаху).
В чем же дело?
Рассмотрим последовательность расстояний, которые должен преодолеть Ахиллес. Сначала он должен пробежать половину расстояния, отделяющего его от черепахи, потом половину половины и т. д. Пусть расстояние равно единице. Получим последовательность: одна вторая, одна четвертая, одна восьмая, одна шестнадцатая и т. д. до бесконечности. Расстояние будет равно сумме бесконечного ряда; должно быть, Зенон полагал, что сумма бесконечного числа слагаемых непременно равна бесконечности (“невозможно коснуться бесконечного числа точек за конечное время”). На самом деле в данном случае это не так: ведь расстояния быстро убывают — это бесконечная геометрическая прогрессия, сумма которой конечна.
Пусть имеем отрезок прямой, длина которого конечна. Разделим его на две равные части; сумма их длин равна длине всего отрезка. Можно разделить каждую из частей еще на две, и так далее до бесконечности. После каждого деления получаются все меньшие отрезки, но сумма их остается постоянной и равной первоначальной длине (еще раз вспомним Паскаля: “Нет геометра, который не полагал бы пространство делимым до бесконечности”). Таким образом, сумма бесконечного числа бесконечно малых есть величина конечная; понимание этого образует рубеж между античным и новоевропейским математическим мышлением.
Один из основных законов формальной (аристотелевой, двузначной) логики — уже упомянутый закон исключенного третьего. Критикуя этот закон, голландский математик Брауэр (1881–1966) указывает на то, что между утверждением и его отрицанием существует еще третья возможность, которую нельзя исключить. Она обнаруживает себя при рассуждениях о бесконечных множествах объектов. Допустим, утверждается существование объекта с определенным свойством. Если множество, в которое входит этот объект, конечно, то можно перебрать все объекты. Это позволит выяснить, какое из следую- щих двух утверждений истинно: “В данном множестве есть объект с указанным свойством” или: “В данном множестве нет такого объекта”. Закон исключенного третьего здесь справедлив.
Но когда множество бесконечно, то объекты его невозможно перебрать. Если в процессе перебора будет найден объект с требуемым свойством, первое из указанных утверждений подтвердится. Но если найти этот объект не удастся, ни о первом, ни о втором из утверждений нельзя ничего сказать, поскольку перебор не проведен до конца. Закон исключенного третьего здесь не действует: ни утверждение о существовании объекта с заданным свойством, ни отрицание этого утверждения не являются истинными. Критика Брауэром закона исключенного третьего привела к созданию нового направления в логике — интуиционистской логики. В последней не принимается этот закон, и отбрасываются все те способы рассуждения, которые с ним связаны. Среди них — доказательства путем приведения к противоречию, или абсурду.
— наука о правильном рассуждении, канон разума, тем самым она составляет самое сердце культуры. Таким образом, своеобразие логики определяет своеобразие культуры. Соотнесем это с идеями О. Шпенглера. “Не существует никакой одной математики, есть лишь множество математик” [133, I, 211]. Это странно звучащее высказывание можно понимать следующим образом: каждой историко-культурной эпохе соответствует своя математика. Древние греки занимались неподвижными как отрезок длиной в две единицы измерения, два в квадрате — это площадь квадрата со стороной два, два в кубе — объем куба со стороной два, а что такое два в четвертой степени, греки не знали. Не знали они ни нуля, ни бесконечности (эти понятия, как было упомянуто, связаны, взаимообусловлены; величина, обратная бесконечно малой — бесконечно велика, и обратно — вспомните о “двойной бесконечности” Паскаля); иррациональные числа, которые можно выразить только бесконечной непериодической десятичной дробью, внушали им священный ужас. Такова и вся их культура — наглядная, статичная, рациональная, скульптурная, чувственно-конкретная, конечная и пластически определенная.
Новоевропейская математика, наоборот, немыслима без понятия бесконечности (и связанных с ним понятий движения и совпадения противоположностей); анализ бесконечно малых — это математический аппарат для описания движения.
Новоевропейская математика стремится описывать изменения и процессы. Все современное естествознание исходит из того, что “” (Whitehead A. The Concept of Nature4 (и человек, как его понимает новоевропейская культура, тоже является процессом). Напротив, Платон полагает, что знание возможно только о неизменных, неподвижных вещах; в текучем знания не бывает” (Кратил 440b), а человек для античности, как пишет А. Ф. Лосев, это прежде всего “хорошо организованное и живое тело” [87]; античная скульптура, изображающая человека именно как тело (в его неподвижности), достигает классических высот и является, как пишет О. Шпенглер, выражением души античной культуры.
прекрасное понимается прежде всего как соразмерное (симметричное, пропорциональное), как правильное соотношение частей и целого (так понимаемое прекрасное как раз и воплощается в античной скульптуре). Тогда как христианские мыслители понимают прекрасное как воплощение Бога; один из атрибутов Бога — бесконечность, отсюда романтическое представление о прекрасном как проявлении бесконечного в конечном (по Шпенглеру, новоевропейская культура (фаустовская душа) наиболее адекватно воплотилась в ). (Эта важная роль категории бесконечности в новоевропейской культуре обусловливает ее эсотеричность и элитарность (см. фрагмент из О. Шпенглера в гл. 2). В самом деле, скульптуру можно видеть глазами и ощупать руками; это доступно каждому; бесконечность — труднопостижимая умозрительная категория, недоступная чувствам; далеко не каждый может освоить, например, анализ бесконечно малых, потому что это наука!)
Вот как современный историк науки П. Гайденко характеризует этот великий перелом в европейском мышлении (речь идет, в частности, о воззрениях выдающегося мыслителя XVI в. Джордано Бруно): “... в XVI в. окончательно сформировалось сознание, представляющее собой прямую противоположность античному: если для древнегреческого философа предел “выше” беспредельного,.. завершенное и целое прекраснее незавершенного и бесконечного, то для ученого эпохи Возрождения беспредельное... бесконечное предпочтительнее перед имеющим конец (предел), становление и непрерывное превращение (возможность) — выше того, что неподвижно... ... для грека космос конечен, так как конечное выше и совершеннее беспредельного; вселенная же Бруно бесконечна, беспредельна, так как бесконечное для него совершеннее конечного.
Как и у Николая Кузанского, у Бруно в бесконечном оказываются тождественными все различия... Все существующее... рассматривается в течении, изменении, взаимопревращении; ничто не равно самому себе, а скорее равно своей противоположности. Это означает, что возможность — становление, движение, превращение, изменение — стала основной категорией мышления (здесь можно вспомнить знаменитое определение романтизма, принадлежащее Шеллингу: “Прекрасное было время… человеческий дух был раскован, считал себя вправе противопологать всему существующему свою действительную свободу и спрашивать не о том, что есть, но что возможно” (Берковский Н. Я. О романтизме и его первоосновах5— А. П.).
Одним из важнейших гносеологических положений философии Бруно является положение о приоритете разума над чувством... Требование Бруно отдать предпочтение разуму перед чувством вполне понятно: центральная категория его мышления — а именно категория бесконечности — не может быть предметом чувства, но лишь предметом мышления” [34, 545–547]. Сравните это с высказыванием Декарта: “Тела познаются не чувствами или способностью представления, а одним только разумом. Они становятся известными не благодаря тому, что их видят или осязают, но благодаря тому, что их разумеют мыслью. Правота присуща не чувству, а одному лишь разуму, отчетливо воспринимающему вещи” [60]. Вспомните о знаменитом принципе Декарта: “Мыслю следовательно существую”. Таким образом, новому складу мышления органически присущ рационализм (уже одного этого было бы достаточно для того, чтобы сделать новоевропейскую культуру элитарной; ведь чувства есть у всех, а высокоразвитый интеллект — лишь у немногих!).
Противоположение имеет прямое отношение к чрезвычайно важному для новоевропейской культуры противостоянию классицизма и романтизма (классицизм декларирует подражание античности, а романтизм идеализирует средневековое христианство).
“…не меньше двух столетий европейское человечество опиралось… на… устойчивые рассудочные, чувственные или рассудочно-чувственные, совершенно неисторические формы красоты. Они и являются содержанием того огромного явления в новой европейской эстетике, которое обычно именуется . Его диалектической противоположностью станет в конце XVIII века …романтизм, культивирующий как раз подвижные исторические и бесконечно уходящие вдаль формы эстетического сознания, еще недоступные двум предшествующим столетиям. Классицизм — это система малоподвижных и отточенных художественных структур, образующих собой пластическое совершенство— это система вечно подвижных и размытых структур, образующих собой беспокойно подвижную и неопределенно стремящуюся бесконечность” (Лосев А. Ф. Конспект лекций по эстетике нового времени. Классицизм // Лит. учеба. 1990. Кн. 4. С. 140).
Итак, О. Шпенглер противопоставляет скульптуру и музыку “…математика, доступная во всей своей глубине очень немногим, сохраняет единственное в своем роде положение среди всех творений духа. Она есть наука строжайшего стиля, как и логика (вспомните вышеизложенные рассуждения о законе исключенного третьего и интуиционистской логике, из которой этот закон исключен — А. П.), но более масштабная и гораздо более содержательная; в том, что касается необходимости ведущего вдохновения и больших конвенций формы в ее развитии, она представляет собою наряду с пластикой и музыкой настоящее искусство… Есть множество миров чисел, так как есть множество культур. Мы обнаруживаем индийский, арабский, античный, западный тип математического мышления… каждый являющийся выражением особого мирочувствования… в котором отражается глубочайшая сущность одной-единственной, а не какой-нибудь еще души, той самой, которая является средоточием именно этой, а не какой-нибудь иной культуры… Каждая философия росла до сих пор в связи с соответствующей математикой.
Сродство форм какой-то одной математики с языком форм соседних больших искусств не подлежит… никакому сомнению. по сути математическим.
В геометрическом анализе и проективной геометрии XVII столетия обнаруживается тот же одухотворенный строй бесконечного (мир античности был конечным и замкнутым (гл. 2). — А. П.) мира, который силится вызвать к жизни, охватить, проникнуть одновременная музыка путем развитой из искусства генерал- баса гармонии, этой геометрии звукового пространства, и родственная ей масляная живопись посредством принципа известной только Западу перспективы, этой прочувствованной геометрии образного пространства… На вершине каждой культуры возникает зрелище великолепной группы больших искусств, хорошо упорядоченных и соединенных лежащим в их основе прасимволом.
Аполлоническая группа — А. П.), к которой принадлежат вазовая роспись, фреска, рельеф, архитектура ордеров, аттическая драма, танец, имеет своим средоточием скульптуру обнаженной статуи.
Фаустовская группа (речь идет о новоевропейской культуре. — А. П.) формируется вокруг идеала чистой пространственной бесконечности. Ее средоточием предстает инструментальная музыка. Отсюда вьются тонкие нити, вплетающиеся во все языки духовных форм и сплетающие инфинитезимальную математику, динамическую физику, пропаганду ордена иезуитов и динамику прославленных лозунгов Просвещения, современную машинную технику, систему кредита и династически- дипломатическую организацию государства…” [133, I, 205–211]. (Курсив мой. — А. П.).
антропоцентризм новоевропейской культуры:
“Современная наука уже давно может объяснить присущий античности примат геометрии, исходя из глубочайших основ античной культуры. И тот факт, что появление теории бесконечно малых в XVII в. связано с выдвижением на первый план человеческого субъекта и с соответствующими теориями бесконечного прогресса, начинают понимать уже многие” [87, 174].
Что есть ? — Центральность человека во Вселенной. “…человек объявлен царем природы”, — пишет А. Ф. Лосев, характеризуя новоевропейскую культуру в ее отличии от античной [87].
Триединство движение — бесконечность — совпадение противоположностей не только лежит в основе науки (математики, философии) нового времени, но имеет непосредственное отношение к характеристике внутреннего мира человека — человека, (вспомните слова Пико делла Мирандолы, приведенные в подгл. 4. 4).
О бесконечности, неисчерпаемости человеческой души сказал еще древнегреческий мыслитель Гераклит:
“Границ души тебе не отыскать, по какому бы пути ты ни пошел: столь глубока ее мера “объем” — в подлиннике стоит “логос”) [122, 231]. О бездне души размышляет Августин Аврелий : “Великая бездна сам человек, “чьи волосы сочтены” у Тебя, Господи, и не теряются у Тебя, и, однако, волосы его легче счесть, чем его чувства и движения его сердца” (Исповедь, IV, XIV, 22) (много позднее это станет одной из центральных тем романтического искусства).
О в человеческой природе пишут Петрарка, Вийон (см. гл. 4) и Державин (ода “Бог”): “Я царь — я раб, я червь — я Бог” [61, 50]. Противоречивость и непостижимость человека (“непостижимое чудовище”!) — предмет размышлений Паскаля (см. гл. 5). О движении как сущности человека говорят Монтень (см. гл. 4) и Паскаль: “Суть человеческого естества — в движении. Полный покой означает смерть” [123, 139].
Для античности человек — это прежде всего хорошо организованное и живое ). “Прасимвол античности, пишет О. Шпенглер, — скульптура, изображающая тело”.
Для средневекового христианства человек — это прежде всего бессмертная душа. Если тело конечно и чувственно конкретно, то душа имеет совершенно иные характеристики, значительно более трудные для осмысления: она бесконечна подвижна и сочетает в себе противоположности. Таким образом, движение, бесконечность и единство противоположностей суть не только ключевые идеи новоевропейской философии, математики и искусства, но и характеристики человеческой души.
Возвращаясь к только что изложенной мысли А. Ф. Лосева, надо добавить, что новоевропейская культура имеет христианские корни (вспомните о том, что атрибут Бога — бесконечность (см. подгл. 3. 3)), и ее антропоцентризм (центральность человека в мире) означает, в частности, пристальное внимание скорее к душе, чем к телу. Отсюда и центральное положение этих трех взаимосвязанных идей в новоевропейской культуре.
— синтез античной и средневековой христианской культур, — начинает осмыслять человека в единстве тела и души. Проблема чрезвычайно трудна и не имеет исчерпывающего и удовлетворительного решения по сей день.
Чтобы изложить результаты самого последнего времени, необходимо напомнить о так называемом принципе дополнительности, который был сформулирован великим физиком ХХ в. Нильсом Бором в 1927 г. Этот принцип представляет собой следующий (после классической немецкой философии, после Гегеля) этап развития учения о противоположностях: Contraria sunt complementa — противоположности суть дополнительности. Н. Бор пришел к идее дополнительности, размышляя о природе света (корпускулярно-волновой дуализм — сочетание в одном объекте свойств частицы (лат. corpuscula) и волны). Иногда (при испускании и поглощении) свет ведет себя как поток частиц, а иногда (интерференция, дифракция, поляризация) — как волна; с точки зрения классической физики имеет место противоречие — волна не может быть частицей, а частица — волной. Такая же двойственность свойств присуща микрочастицам, например, электронам.
вещество (имеющее прерывное, дискретное строение, — состоящее из атомов) и непрерывное поле, благодаря которому осуществляется взаимодействие тел. В современной физике, в частности, в квантовой механике (теории движения микрочастиц) это разделение потеряло абсолютный смысл: микрочастицы проявляют волновые свойства, а каждому полю соответствуют кванты — фотоны, “частицы” света). Кванты поля во многом подобны частицам. (Мякишев Г. Я., Буховцев Б. Б. Физика. Учебн. пособие для 10 кл. средней шк. М., 1972).
“... странное поведение света все-таки поддается полному описанию с помощью двух классических образов, да только абсолютно несовместимых! Сочетается классически несочетаемое, и это-то приносит успех! Сохраняется макрословарь, но микромир требует своей грамматики. и эта грамматика заключается в том, что несочетаемым образам и понятиям разрешено ДОПОЛНЯТЬ друг друга. Так устроено наше знание. Уже не классическое, но уже и не беспомощное перед своеобразием глубин материи. Доведенная до крайности, беда противоречивости превращается в БЛАГО ДОПОЛНИТЕЛЬНОСТИ!” (Данин Д. С. Труды и дни Нильса Бора. М., 1985. С. 57–58). Частными случаями дополнительности являются соотношения неопределенности Гейзенберга (Волькенштейн М. В. Дополнительность, физика и биология6).
В работе “Дискуссии с Эйнштейном о проблемах теории познания в атомной физике (1949)” Н. Бор пишет о том, что истины бывают двух видов: тривиальные (плоские) и глубокие. “К одному роду истин относятся такие простые и ясные утверждения, что противоположные им, очевидно, неверны. Другой род, так называемые “глубокие истины”, представляют, наоборот, такие утверждения, что противоположные им тоже содержат глубокую истину” (Бор Н. Атомная физика и человеческое познание. М., 1961). Это означает, что содержательность утверждения проверяется тем, может ли оно быть опровергнуто.
“Многогранность личности Бора” говорит об этом более подробно: “При изучении абстрактных философских проблем Бор обращал особое внимание на возможность двойственного толкования, заключенную в самих значениях слов. Эта двойственность может определять истинность или ложность высказывания. Бор считал, что высшая мудрость должна быть обязательно выражена такими словами, смысл которых нельзя определить однозначно. Следовательно, истинность высшей мудрости является не абсолютной, а только относительной в соответствии с одним из значений двузначных слов: поэтому противоположное высказывание также правомерно и мудро. Бор пояснял это на следующем примере: “Бог есть” — выражение высшей мудрости и правды, и, наоборот, “Бога нет” — тоже выражение высшей мудрости и правды” (Нильс Бор. Жизнь и творчество: Сб. ст. М., 1967). Закон исключенного третьего, очевидно, применим к тривиальным истинам, но к глубоким истинам его применить нельзя.
На вопрос “Что дополнительно понятию истины?” Бор ответил: “Ясность”.
“Бор вел огромную и напряженную работу по исследованию применения понятия дополнительности в других областях знаний. Эту задачу он считал не менее существенной, чем чисто физические исследования” (Мигдал А. Б. Квантовая физика и Нильс Бор. М., 1987. С. 48). Эти идеи развиты в статье 1954 г. “Единство знаний”: Бор пишет о проблемах психологии и культуры, о дополнительности интуиции и логики, искусства и науки, мысли и действия, серьезности и шутливости, справедливости и милосердия.
“Особенно ярким примером является взаимоотношение между теми ситуациями в которых мы обдумываем мотивы наших действий, и теми, когда мы испытываем чувство решимости.
В нормальной жизни такой переход от одного состояния к другому более или менее осознается интуитивно. Но психиатрам хорошо известны и симптомы, характеризуемые как “раздвоение личности”, которое может привести к ее распаду. Тот факт, что для описания различных, одинаково важных сторон человеческой души приходится применять различные, как бы исключающие друг друга характеристики, и в самом деле представляет замечательную аналогию с положением в атомной физике, где определение дополнительных явлений требует применения совсем разных элементарных понятий. Прежде всего самое слово “сознательный” относится к опыту, который может удержаться в памяти; это обстоятельство подсказывает нам сравнение между сознательным опытом и физическими наблюдениями. В этой аналогии невозможность придать недвусмысленное содержание идее подсознания соответствует невозможности наглядного (модельного) толкования квантовомеханического аппарата (вспомните о том, что понятие “подсознание” — центральное в теории Фрейда, и о том, какую значительную роль сыграл фрейдизм в культуре ХХ в. (см. гл. 6. — А. П.). Между прочим можно сказать, что психоаналитическое лечение неврозов восстанавливает равновесие в содержании памяти пациента тем, что приносит ему новый сознательний опыт, а не тем, что помогает ему измерить бездны его подсознания...
После того как я рассмотрел некоторые научные проблемы, имеющие отношение к единству знаний, я хочу обратиться к вопросу о том, существует ли поэтическая, или духовная, или культурная истина, отличная от истины научной... Возвращяясь к нашей мысли о зависимости между нашими средствами выражения и областью интересующего нас опыта, мы не можем миновать вопрос о взаимоотношении между наукой и искусством. Причина, почему искусство может нас обогатить, заключается в его способности напоминать нам о гармониях, недосягаемых для систематического анализа. Можно сказать, что литературное, изобразительное и музыкальное искусства образуют последовательность способов выражения, и в этой последовательности все более полный отказ от точных определений, характерных для научных сообщений, предоставляет больше свободы игре фантазии. В частности, в поэзии эта цель достигается сопоставлением слов, связанных с меняющимся восприятием наблюдателя, и этим эмоционально объединяются многообразные стороны человеческого познания...
... равновесие между серьезностью и шуткой, типичное для всякого истинно художественного исполнения, напоминает нам о дополнительных аспектах, бросающихся в глаза в детской игре и не менее ценимых взрослыми. В самом деле, если мы будем стараться всегда говорить совершенно серьезно, мы рискуем очень скоро показаться нашим слушателям и себе самим смехотворно скучными; а если мы попробуем все время шутить, мы скоро обнаружим (да и наши слушатели тоже), что находимся в унылом настроении шутов в драмах Шекспира.
При сравнении между науками и искусствами, конечно, нельзя забывать, что в науках мы имеем дело с систематическими согласованными усилиями, направленными к накоплению опыта и разработке представлений, пригодных для его толкования; это похоже на переноску и подгонку камней для постройки. В то же время искусство представляет собой более интуитивные попытки отдельного лица вызвать чувства, напоминающие о некоторой душевной ситуации в целом. Здесь мы подходим к той точке, где вопрос о единстве знаний, как и самое слово “истина”, становится неоднозначным. Действительно, в отношении к духовным и культурным ценностям мы тоже не должны забывать о проблемах теории познания, которые связаны здесь с правильным балансом между нашим стремлением к всеобъемлющему взгляду на жизнь во всем ее многообразии и нашими возможностями выражать свои мысли логически связным образом...
границей между оценкой человеческих ценностей и общими положениями, на основании которых о них судят. Конечно, всякое устойчивое человеческое общество нуждается в честной игре, установленной мудрыми правилами; и в то же время жизнь без привязанности к семье и друзьям была бы, очевидно, лишена одной из своих самых драгоценных и привлекательных сторон. Общую цель всех культур составляет самое тесное сочетание справедливости и милосердия, какого только можно достигнуть; тем не менее следует признать, что в каждом случае, где нужно строго применить закон, не остается места для проявления милосердия, и наоборот, доброжелательство и сострадание могут вступить в конфликт с самыми принципами правосудия” (Бор Н. Атомная физика и человеческое познание. М., 1961. С. 108–113).
Уже было сказано о том, что законы классической логики суть законы правильного мышления и, конечно, они тесно связаны с методологией естественных наук, бурно развивавшихся в XVII–XIX вв. Например, классическая физика прекрасно согласуется с классической (аристотелевой, двузначной) логикой.
Математическая схема квантовой теории, развитой в ХХ в., требует расширения или модификации классической логики.
Рассмотрим, например, такую ситуацию: в ящике, разделенном стенкой на две равные части, находится атом. Пусть в стенке имеется отверстие, так что атом может случайно перемещаться из одной половины ящика в другую. Тогда, согласно классической логике, атом может находиться или в правой, или в левой половине ящика. Не существует никакой третьей возможности, tertium non datur “Однако в квантовой теории необходимо добавить, что имеются еще другие возможности, которые представляют собой странного рода смеси обеих ранее перечисленных возможностей. Эти смеси необходимы, чтобы объяснить результаты экспериментов. Можно, например, наблюдать свет, рассеянный атомом. При этом возможно провести три опыта. В первом атом заключен только в левой половине ящика (например, благодаря тому, что отверстие закрыто), и измеряется распределение интенсивностей рассеянного света. Во втором опыте атом заключен только в правой половине ящика, и снова измеряется рассеяние света. Наконец, в третьем опыте атом может свободно перемещаться по всему ящику туда и сюда, и опять с помощью измерительных приборов исследуется распределение интенсивностей рассеянного света.
Распределение интенсивностей в третьем опыте (согласно воззрениям классической физики) должно было бы представлять собой смесь обоих предыдущих распределений интенсивности (в отношении, соответствующем промежуткам времени, которые атом проводит в одной и другой половине). Однако эксперимент показывает, что это не так” (Гейзенберг В. Физика и философия. М., 1989. С. 114–115).
В классической механике, рассматривающей движение тела в пространстве, указывают его координаты и скорость в каждый момент времени. В квантовой механике принципы описания иные: можно указать только вероятность нахождения частицы в определенной области пространства (это связано с принципом неопределенности Гейзенберга, который является частным случаем принципа дополнительности. К микрочастицам, обладающим волновыми свойствами, понятия классической механики (в частности, понятия координаты и импульса) можно применять лишь в ограниченной степени: поэтому в квантовой механике существуют принципиальные неточности в определении пространственного положения (координаты) и величины импульса частицы. Неточность в определении координаты частицы, умноженная на неточность в определении проекции импульса больше или равна некоторой постоянной величине. Таким образом, чем точнее определены координаты частицы, тем менее точно определены значения проекций ее импульса. Точно определенным координатам частицы соответствует полная неопределенность в значениях проекций ее импульса (Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов. М., 1979. С. 719).
механикой (и классической логикой), но это только предельные случаи (в данном случае классическая логика является частным случаем неклассической).
Между ними простирается целый спектр других возможных ситуаций: с вероятностью 0,1 атом находится в левой половине и 0,9 — в правой, 0,2 — в левой и 0,8 — в правой и т. д. (сумма вероятностей должна быть равна единице, поскольку атом с достоверностью находится в ящике). При этом понятие “дополнительности” можно ввести с помощью следующего определения: всякое высказывание, не тождественное ни с одним из пары альтернативных высказываний — “атом с достоверностью находится в правой половине”, “атом с достоверностью находится в левой половине”, — будет называться дополнительным по отношению к этим высказываниям. “Для всякого дополнительного высказывания вопрос о том, находится ли атом слева или справа, неопределен. Однако выражение “неопределенно” никоим образом не эквивалентно выражению “неизвестно”. “Неизвестно” означало бы, что атом в действительности находится или слева, или справа, и что мы только не знаем, где он находится. А “неопределенно” указывает на отличную от этого ситуацию, которая может быть описана с помощью дополнительного высказывания”7.
Итак, подведем итог: принцип неопределенности, сформулированный В. Гейзенбергом, является частным случаем Бора, согласно которому “для воспроизведения в знаковой системе целостного явления необходимы взаимоисключающие, дополнительные классы понятий. Это требование эквивалентно расширению логической структуры языка физики. Бор использует, казалось бы, очень простое средство: признается допустимым взаимоисключающее употребление двух языков, каждый из которых базируется на обычной логике. Они описывают исключающие друг друга физические явления, например, непрерывность и атомизм световых явлений и т. п. ... Бор сам хорошо понимал методологическое значение сформулированного им принципа: “... целостность живых организмов и характеристика людей, обладающих сознанием, а также и человеческих культур представляют черты целостности, отображение которых требует типично дополнительного способа описания”. ... Принцип дополнительности — это, собственно, признание того, что четко логически построенные теории действуют как метафора: они задают модели, которые ведут себя и как внешний мир, и не так. Одной логической конструкции оказывается недостаточно для описания всей сложности микромира. Требование нарушить общепринятую логику при построении картины мира со всей очевидностью впервые появилось в квантовой механике — и в этом ее особое философское значение”8 (Налимов В. В. Вероятностная модель языка. М., 1979. С. 102–103).
Современный исследователь пишет: “Соответствующей дополнительностью на уровне человека будет образ ньютоно-картезианской биологической машины и неограниченного поля сознания… Хотя это кажется абсурдным и невозможным с точки зрения классической логики, человеческая природа демонстрирует интересную двойственность. Иногда она приземляет себя до механических интерпретаций, приравнивая человека к его телу и функциям организма. В других случаях она выявляет совершенно иной образ, предполагая, что человек может функционировать как безграничное поле сознания, трансцендирующее материю, пространство, время и линейную причинность. Для того, чтобы описать человека всесторонним и исчерпывающим способом мы должны принять парадоксальный факт, что он есть одновременно и материальный объект, т. е. биологическая машина, и обширное поле сознания …За последние три десятилетия значительные наработки в области математики, лазерной технологии, голографии, квантово-релятивистской физики и в исследованиях мозга привели к открытию новых принципов, открывающих далеко идущие перспективы для современных исследований сознания и для науки в целом. Эти принципы были названы холономными, холографическими или холограммными (“холос”(греч.) — весь, полный, целый. — … У современного холономного подхода ко Вселенной есть исторические предшественники в древней индийской и китайской философии, в монадологии великого немецкого философа и математика Готфрида Вильгельма фон Лейбница…
Трансценденция конвенциального различия частей и целого, являющаяся главным достижением холономной модели, — это сущностная характеристика самых разных систем философии.
Поэтический образ ожерелья ведического бога Индры — прекрасная иллюстрация этого принципа. В “Аватамсака-сутре” записано: “В небесах Индры есть, говорят, нить жемчуга, подобранная так, что если глянешь на одну жемчужину, то увидишь все остальные отраженными в ней. И точно так же каждая вещь в мире не есть просто она сама, а заключает в себе все другие вещи и на самом деле есть все остальное… Сходный образ древнекитайской традиции можно найти в буддистской школе хуаянь; это холистический взгляд на Вселенную, воплощающий одно из наиболее глубоких прозрений, когда-либо достигнутых человеческим разумом. Императрица Ву, которая оказалась не в состоянии одолеть сложности хуаяньской литературы, попросила Фа Цанга, одного из основателей школы, дать ей практическую и простую демонстрацию космической взаимозависимости. Фа Цанг сначала подвесил горящий светильник к потолку комнаты, уставленной зеркалами, чтобы показать отношение Единого к многому. Затем он поместил в центре комнаты маленький кристалл и, показав, что все окружающее отражается в нем, проиллюстрировал, как в Предельной Реальности бесконечно малое содержит бесконечно большое, а бесконечно большое — бесконечно малое. Проделав все это, Фа Цанг заметил, что, к сожалению, эта статичная модель неспособна отразить вековечное, многомерное движение во Вселенной и беспрепятственное взаимное проникновение Времени и Вечности, а также прошлого, настоящего и будущего” (Гроф С. За пределами мозга. Рождение, смерть и трансценденция в психотерапии. М., 2001. С. 91–95)9.
Применительно к человеку это означает актуализацию древней доктрины микрокосма и макрокосма, подобия человека и Вселенной взаимно однозначное соответствие между элементами бесконечного множества и его части. Коротко говоря, и Вселенной, и внутреннему миру человека присуща бесконечность — в этом они подобны.
В ХХ в. одновременно с квантовой механикой возникает и нечто принципиально новое в области логики (уже было упомянуто о брауэровской критике закона исключенного третьего). Классическая аристотелева логика была двузначной: истина и ложь были двумя возможными вариантами (tertium non datur — третьего не дано). В неклассической (в частности, квантовой) логике это не так10
Исторически первой была трехзначная логика Лукасевича (“истинно”, “ложно”, “возможно”) (1920), позднее были разработаны, например, многозначная логика Поста (1921) и трехзначная логика Бочвара (1938) (Ішмуратов А. Т. Вступ до філософської логіки. К., 1997).
механистические представления. Считалось, что коль скоро начальное состояние системы задано, ее дальнейшая эволюция во времени точно предсказуема. Суть детерминизма наиболее полно выразил выдающийся французский математик и физик Пьер Симон Лаплас (1749– 1827) в известном отрывке из “Аналитической теории вероятностей”: “Разумное существо, которое в каждый данный момент знало бы все движущие силы природы и имело бы полную картину состояния, в котором природа находится, могло бы (если бы только его ум был в состоянии проанализировать эти данные) выразить одним уравнением как движение самых больших тел мира, так и движение мельчайших атомов.
Ничто не осталось бы для него неизвестным, и оно могло бы обозреть одним взглядом как будущее, так и прошлое” (лапласов детерминизм). Иначе говоря, если бы такое существо знало начальные состояния всех индивидуальных частей системы (в частности, положения и скорости всех образующих систему частиц) и взаимодействия между ними, то оно могло бы предсказать состояние системы в любой момент в будущем.
С возникновением в 20-х годах ХХ в. квантовой теории стало ясно, что предсказывать с абсолютной точностью положения и скорости частиц невозможно даже в принципе (ведь соотношение неопределенностей Гейзенберга показывает, что скорость и положение частицы невозможно одновременно измерить с абсолютной точностью). . Это имеет особенно важное значение в тех случаях, когда микроскопические явления усиливаются настолько, что обретают макроскопические размеры (например, в биологии квантовые флуктуации могут вызывать мутации) (Хакен Г. Синергетика. Иерархии неустойчивостей в самоорганизующихся системах и устройствах. М., 1985. С. 43–44).
Итак, классическая механика исходит из альтернативной дилеммы необходимость — случайность и занимается исключительно областью необходимости. Квантовая механика предсказывает некий ряд разных результатов и дает вероятность каждого из них. Таким образом, квантовая механика вносит в науку элемент непредсказуемости или случайности (Хокинг С. От большого взрыва до черных дыр. Краткая история времени. М., 1990).
Выдающийся ученый нашего времени Нобелевский лауреат Илья Пригожин пишет о величайшем физике ХХ в. Альберте Эйнштейне: “Эйнштейн придерживался глубоко пессимистических взглядов на человеческую жизнь. Он жил в особенно трагический период человеческой истории, в период фашизма, антисемитизма и двух мировых войн. Но его видение физики отождествлялось с наивысшим триумфом человеческого разума над миром, триумфом, удовлетворяющим страстному стремлению отделить чистое объективное знание от области неопределенного и субъективного. Это стремление может объяснить превалирование бытия над становлением на протяжении большей части истории физики (курсив мой. — А. П.). (Действительно, в продолжение по меньшей мере трех столетий, с XVII по XIX в., в центре внимания классической науки — мир без времени, неизменные, неподвижные объекты, (“Закат Европы” О. Шпенглера начинается с фундаментального противопоставления ставшее — становление). Только во второй половине XIX в. идея развития начинает оказывать все более значительное воздействие на естественные науки. “Глава Брюссельской научной школы И. Р. Пригожин называет эту ситуацию “переоткрытием времени”. Для классического подхода время представляет собой лишь внешний количественный параметр и, что самое главное, — полностью обратимо. Обратимость здесь, по существу, означает отсутствие времени, так как снимает различие между прошлым, настоящим и будущим.
В этом смысле можно говорить о “безвременной”, то есть безразличной к направлению времени научной картине мира. Известно следующее высказывание Эйнштейна: “Для нас, убежденных физиков, различие между прошлым, настоящим и будущим всего лишь иллюзия, хотя и весьма устойчивая” (EinsteinA. Besso M. Correspondance 1903–1955. Paris, 1972. Р. 539)…
“без времени” встает представление о мире развивающемся. Термодинамика с ее понятием энтропии и дарвинизм с его понятием эволюции — первые научные концепции, которые несли в себе содержательное и качественное представление о времени… В отличие от “физики существующего” (being) рождается “физика возникающего” или “физика становления” (becoming) (Пригожин И. От существующего к возникающему. М., 1985.)” (Аркадьев М. А. Временные структуры новоевропейской музыки. М., 1992. С. 99–100). Вообще говоря, статическое, “безвременное”, и динамически-процессуальное направления противоположны друг другу, но эта противоположность должна пониматься в духе принципа дополнительности Бора. — А. П.). Французский философ Эмиль Мейерсон усматривал в попытке сведения природы к тождеству основную движущую силу западной науки (Meyerson E. Identity and Reality. — L.: Allen and Unwin, 1930.) Эта движущая сила парадоксальна, подчеркнул Мейерсон, так как стремление к идентификации уничтожает то, что должно познать. Что остается от нашего отношения к миру, если этот мир сводится к некоторой геометрической истине?...
Но и то, что полностью случайно, также лишено реальности. Мы можем понять отказ Эйнштейна от случая как от универсального ответа на наши вопросы. (“Я не верю, что Старик играет в кости”, — говорил Эйнштейн о Боге. — А. П.). Мы должны отыскать узкую тропинку, затерявшуюся где-то между двумя концепциями, каждая из которых приводит к отчуждению: концепцией мира, управляемого законами, не оставляющими места для новации и созидания, и концепцией, символизируемой Богом, играющим в кости, концепцией абсурдного, акаузального мира (т. е. такого, в котором отсутствует причинно-следственная связь. — А. П.), в котором ничего нельзяпонять...
То, что возникает буквально на наших глазах, есть описание, промежуточное между двумя противоположными картинами — детерминистическим миром и произвольным миром...
вероятностными представлениями. Ассоциируемые теперь с неустойчивостью, будь то неустойчивость на микроскопическом или на макроскопическом уровнях, несводимые вероятностные представления оперируют с возможностью событий, но не сводят реальное индивидуальное событие к выводимому, предсказуемому следствию.
Такое разграничение между тем, что предсказуемо и управляемо, и тем, что непредсказуемо и неуправляемо, возможно, удовлетворило бы эйнштейновский поиск познаваемости.
Прокладывая тропинку, избегающую драматической альтернативы между слепыми законами и произвольными событиями, мы обнаруживаем, что значительная часть конкретного мира вокруг нас до сих пор “ускользала из ячеек научной сети”, если воспользоваться выражением Уайтхеда. Перед нами открылись новые горизонты...” (Пригожин И., Стенгерс И. Время, хаос, квант. К решению парадокса времени. М., 1999. С. 260–263).
Итак, мы видим, что современная картина мира возникает в результате диалектического синтеза двух противоположностей; подобного рода синтезом необходимости и случайности является вероятность.
